https://doi.org/10.1351/goldbook.10116
Decomposition of a three-way data matrix into a three-way core matrix, and three, two-way loadings matrices.
Notes:
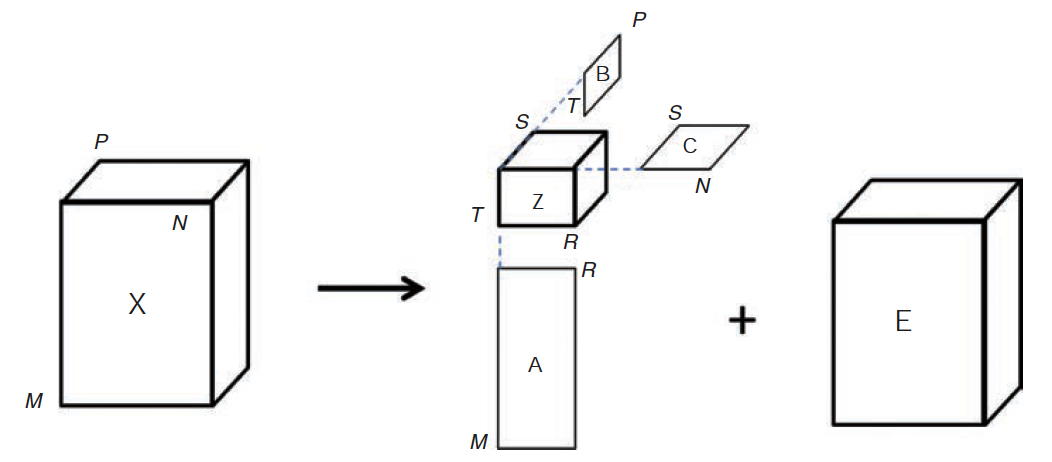
- A representation of the Tucker3 model is \[x_{ijk} = \sum\limits_{r\,=\,1}^R \sum\limits_{s\,=\,1}^S \sum\limits_{t\,=\,1}^T a_{ir}b_{js}{c_{kt}z_{rst} + e_{ijk}}\] where \(x_{ijk}\) is the data matrix, \(a_{ir}\), \(b_{js}\), \(c_{kt}\) are the loadings matrices, and \(z_{rst}\) is the core matrix. \(e_{ijk}\) is the residual matrix.
- A graphical representation of the Tucker3 model is
See: parallel-factors analysis
Source:
PAC, 2016, 88, 407. 'Vocabulary of concepts and terms in chemometrics (IUPAC Recommendations 2016)' on page 425 (https://doi.org/10.1515/pac-2015-0605)
PAC, 2016, 88, 407. 'Vocabulary of concepts and terms in chemometrics (IUPAC Recommendations 2016)' on page 425 (https://doi.org/10.1515/pac-2015-0605)