https://doi.org/10.1351/goldbook.10103
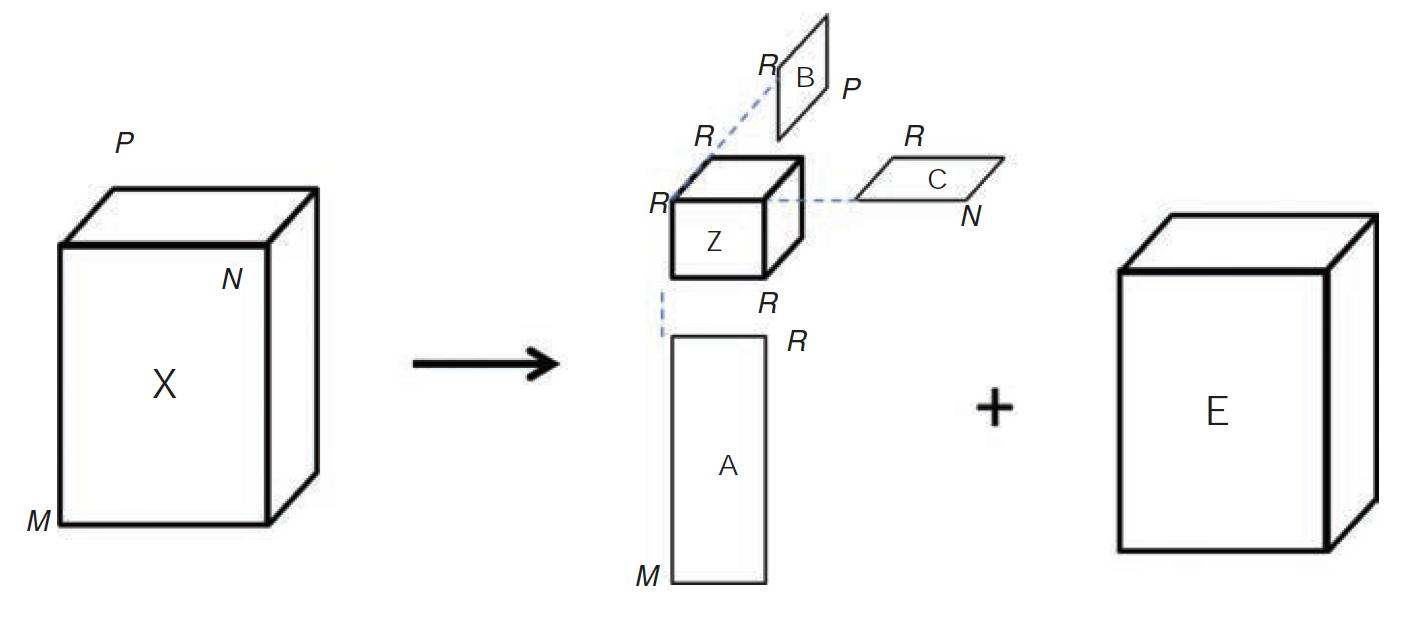
Decomposition of a three-way data matrix into the sum of sets of two-way loadings matrices.
Notes:
- The PARAFAC model is also known as Canonical Decomposition (CANDECOMP).
- A representation of PARAFAC is \(x_{ijk} = \sum\limits_{r\,=\,1}^R a_{ir}b_{jr}c_{kr} + e_{ijk}\), where \(x_{ijk}\) is \(i\),\(j\),\(k\)-th element of the data matrix, and \(a_{ir}\), \(b_{jr}\), \(c_{kr}\) are the components of the loadings matrices. \(e_{ijk}\) is the \(i\),\(j\),\(k\)-th element of residual matrix.
- PARAFAC is a special case of the Tucker3 model (see Tucker tri-linear analysis) where the core matrix is the identity matrix, and \(r = s = t = R\) .
- A schematic representation of the PARAFAC model is