https://doi.org/10.1351/goldbook.09625
Number of generations of the hypothetical dendrimer molecule that would present the same ratio of constitutional repeating units to core unit.
Notes:
- The number of pseudo-generations can be a decimal number, while the number of generations of a dendrimer molecule is an integer.
- In hyperbranched polymers obtained by the \({\rm{AB}}_{x}\mbox{-}\rm{type}\) monomer + \({\rm{B}}_{y}\mbox{-}\rm{type}\) monomer polycondensation approach, where \(\rm{A}\) and \(\rm{B}\) represent mutually reactive groups, the number of pseudo-generations \(n\) can be calculated by solving the equation: \[r = y(x^n - 1)/(x - 1)\], where \(r\) is the mole ratio of \({\rm{AB}}_{x}\mbox{-}\rm{type}\) monomer to \({\rm{B}}_{y}\mbox{-}\rm{type}\) monomer in the initial monomer mixture. See the figure for an example of \({\rm{AB}}_2\) and \({\rm{B}}_{3}\mbox{-}\rm{type}\) monomers (\(x = 2\) and \(y = 3\)).
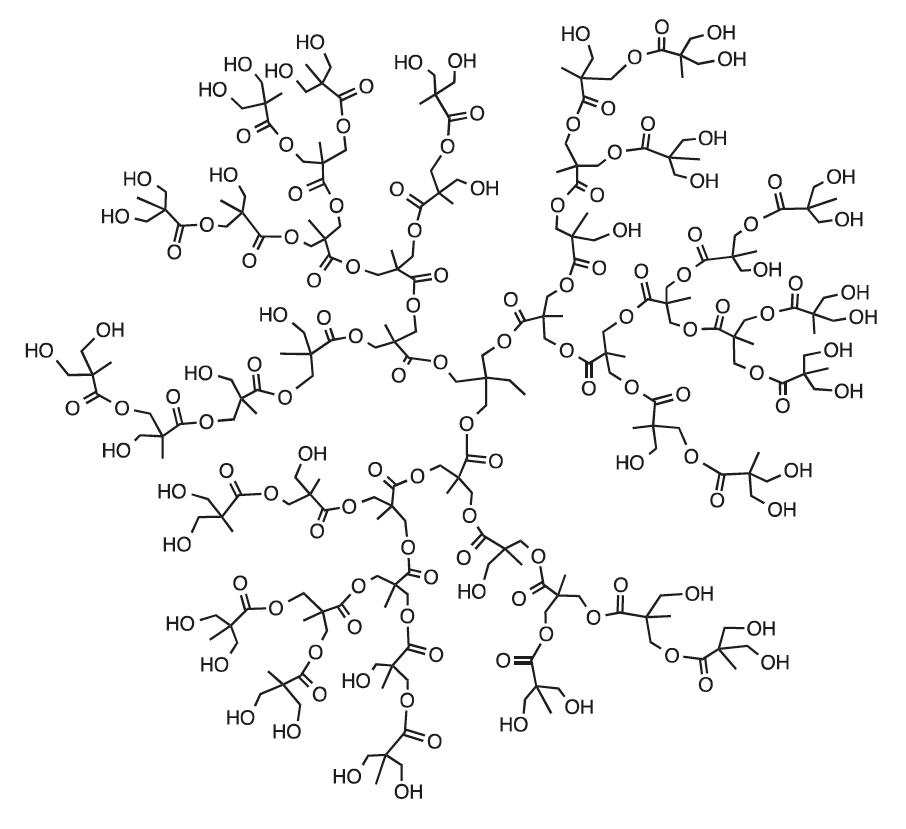
Idealized representation of an aliphatic hyperbranched polyester macromolecule obtained by one-step bulk polyesterification of 3-hydroxy-2-(hydroxymethyl)-2-methylpropanoic acid (\({\rm{AB}}_{2}\mbox{-}\rm{type}\) monomer) and 2-ethyl-2-(hydroxymethyl)propane-1,3-diol (\({\rm{B}}_{3}\mbox{-}\rm{type}\) molecule).
- The use of the terms generation and number of generations for a hyperbranched polymer is not acceptable.
Source:
PAC, 2019, 91, 523. 'Nomenclature and terminology for dendrimers with regular dendrons and for hyperbranched polymers (IUPAC Recommendations 2017)' on page 533 (https://doi.org/10.1515/pac-2016-1217)
PAC, 2019, 91, 523. 'Nomenclature and terminology for dendrimers with regular dendrons and for hyperbranched polymers (IUPAC Recommendations 2017)' on page 533 (https://doi.org/10.1515/pac-2016-1217)